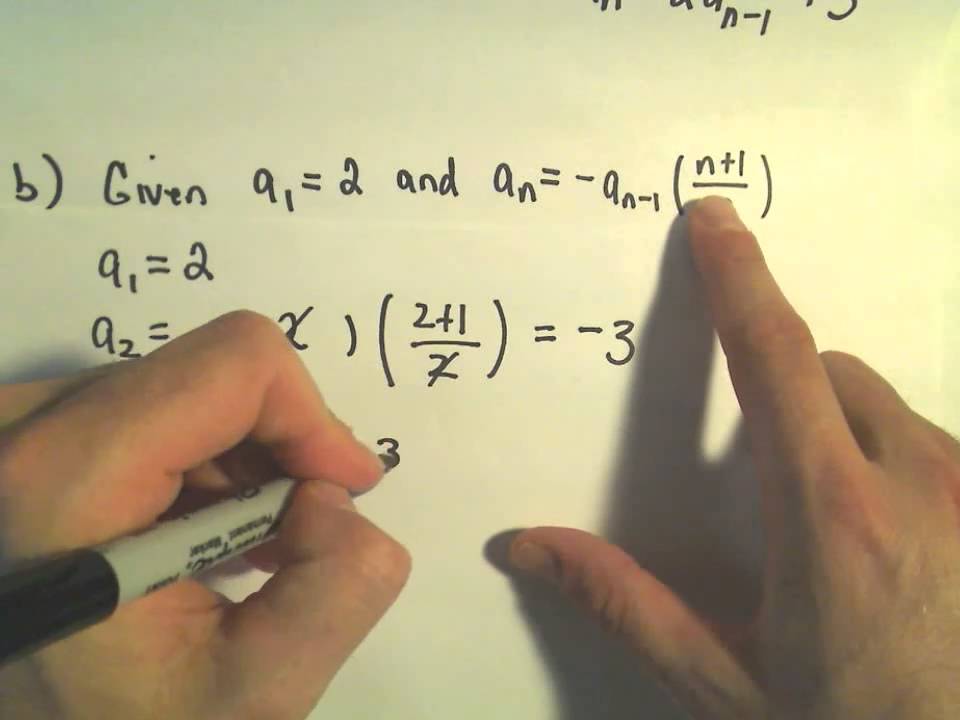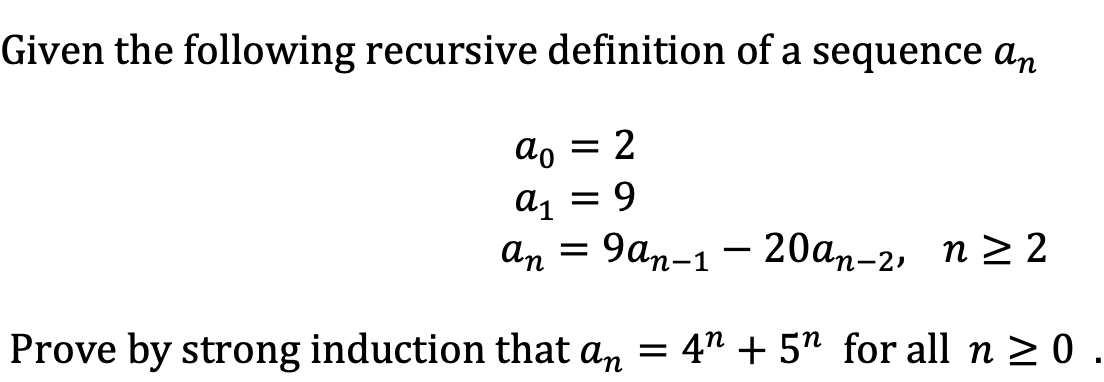Mathematical Induction
Answered: Suppose we have a recursive sequence… | bartleby
Proof by Induction - Recursive Formulas - YouTube
How to: Prove by Induction - Proof of a Recurrence Relationship - YouTube
discrete mathematics - How to find the recursive definition of this function and prove by induction. - Mathematics Stack Exchange
Proof by Induction: Recursive function with multiple initial terms - YouTube
calculus - Showing that a recursive sequence is monotonous by using induction - Mathematics Stack Exchange
Chapter 4 Induction and Recursion
Answered: Suppose that h, is a sequence… | bartleby
Strong Induction, Recursive function, Inequality | Sumant's 1 page of Math
How to show that following [math](a_n)[/math]real recursive sequence [math]a_{n + 1} = \dfrac{a_{n}^2 + 2 a_{n} - 3}{a_{n} + 1}[/math] with [math]a_1 = 4[/math] is increasing via mathematical induction? Is this recursive
Mathematical Induction Inequality Proof with Recursive Function - YouTube
Proof by Induction - Recurrence relations (3) FP1 Edexcel Maths A-Level - YouTube
Mathematical Induction Proof with Recursively Defined Function - YouTube
Solved Strong Induction Prove the following statement using | Chegg.com
Solved 3.Use strong induction. Consider the sequence | Chegg.com
Solved 5. Given the following recursive definition of a | Chegg.com
Recursive Sequences - YouTube
inductive proof for recursive sequences - YouTube
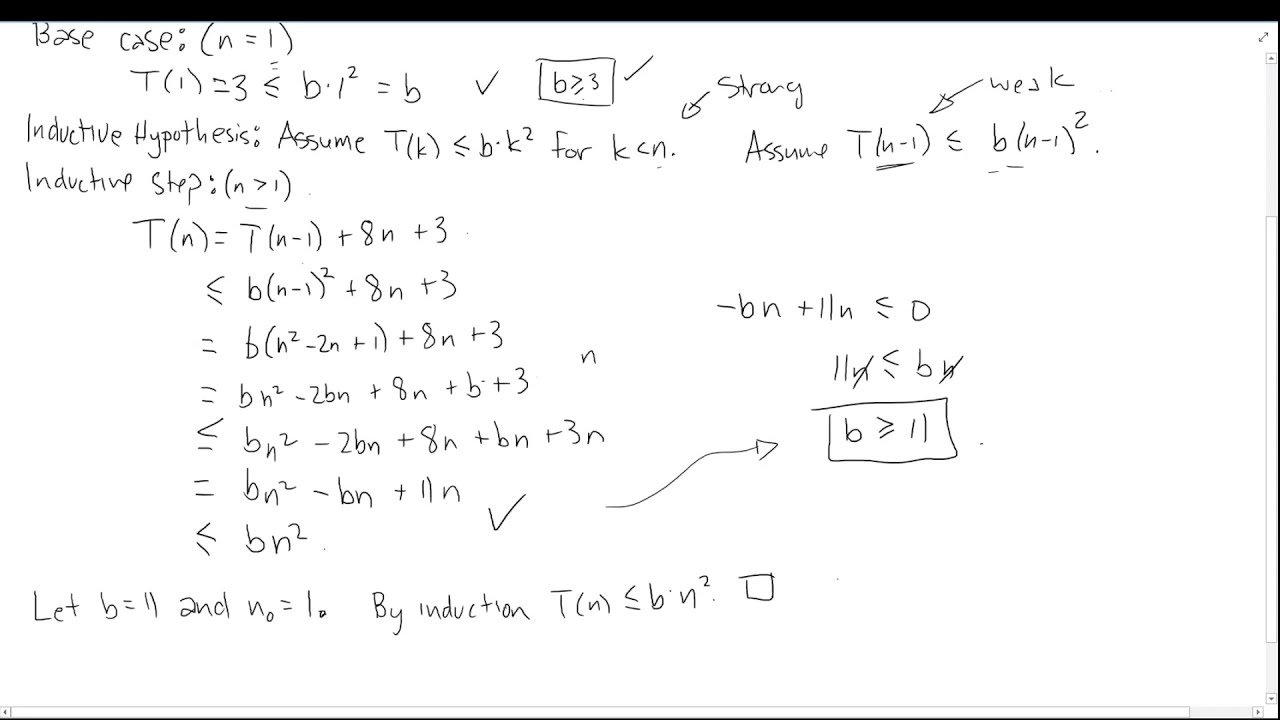
Using strong induction to prove bounds on a recurrence relation - Discrete Math for Computer Science - YouTube
proof writing - Help with induction step of proving a recursive definition / sequence - Mathematics Stack Exchange
Induction and Recursion - ppt download
Solved I'm not sure how to do it but I know that a) should | Chegg.com
Solved Given the following recursive definition of a | Chegg.com
Proof by Induction - Recursive Formulas - YouTube
